Carga
en estrella con neutro accesible
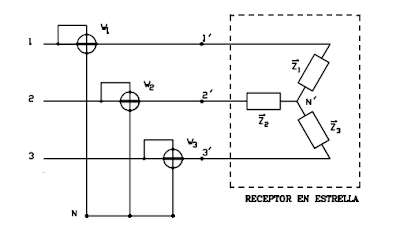
Si tenemos un receptor trifásico,
compuesto por tres impedancias conectadas en estrella
y con neutro, la potencia
absorbida por las tres impedancias se puede medir mediante Z1, Z2
y Z3 tres vatímetros conectados según la
figura siguiente:
Que coinciden con las potencias
activas consumidas por cada impedancia respectivamente
W1 = PZ1 , W2 = PZ2 , W3 = PZ3
por lo que la potencia activa
total consumida por este receptor, que es la suma de las potencias activas
consumidas por cada impedancia, coincide con la suma de las lecturas de los
vatímetros conectados según la figura anterior.
P = PZ1 + PZ2 + PZ3 = W1 + W2 + W3
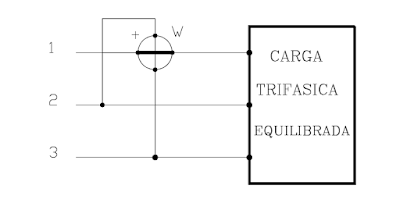
Si las tres impedancias son
iguales tendremos un sistema equilibrado en
Z1 = Z2 = Z3 intensidades y tensiones, por lo que I1 = I2
= I3 y n1= n2= n3 , por consiguiente solo se necesita un vatímetro, W , para
medir la potencia activa total, que será:
P = 3 W
Carga
en estrella con neutro NO accesible.
El caso de este receptor que solo
dispone de tres conductores (tres fases), la medida de la potencia activa total
consumida por el receptor se puede obtener mediante tres vatímetros montados
según el esquema de la figura, donde vemos que se ha formado un neutro
artificial con las bobinas voltimétricas de los vatímetros.
Carga
en triángulo con fases accesibles.
Para un sistema de cargas
conectadas en triángulo con fases accesibles, un Z12, Z23
y Z31 sistema de medida de potencia
activa total, puede verse en la figura.
La potencia activa total
consumida por la carga trifásica en triángulo, será la suma de las potencias de
cada uno de los tres sistemas monofásicos que lo forman:
P = PZ12 + PZ23 + PZ31
donde PZ12 +PZ23 y PZ31 son las
potencias activas consumidas por las impedancias Z12,
Z23 y Z31 respectivamente.
La lectura del vatímetro W1 coincide
con la potencia media o activa consumida por la impedancia Z12
W1 = U1'2' I1'2' Cos (U1'2', I1'2')
= PZ12
de igual manera la lectura de los
vatímetros W2 y W3 son:
W2 = U2'3' I2'3' Cos (U2'3', I2'3')
= PZ23
W3 = U3'1' I3'1' Cos (U3'1', I3'1')
= PZ31
Esto
implica que la suma de las lecturas de los tres vatímetros nos da la potencia
activa total consumida por el receptor en triángulo.
P
= W1 + W2 + W3
Si
las tres impedancias fueran iguales, la lectura de los tres vatímetros Z12 ' Z23 ' Z31
también sería la misma, W1 = W2 = W3, por lo que con un solo vatímetro, W,
sería suficiente para medir la potencia activa, siendo:
P
= 3 W.